Lista Auxílio para os alunos dos 3º anos - Geometria Analítica

Geometria Analítica I

Fonte: http://www.paulomarques.com.br
1 - Introdução
A Geometria Analítica é uma parte da Matemática , que através de processos particulares , estabelece as relações existentes entre a Álgebra e a Geometria. Desse modo , uma reta , uma circunferência ou uma figura podem ter suas propriedades estudadas através de métodos algébricos .
Os estudos iniciais da Geometria Analítica se deram no século XVII , e devem-se ao filósofo e matemático francês René Descartes (1596 - 1650), inventor das coordenadas cartesianas (assim chamadas em sua homenagem), que permitiram a representação numérica de propriedades geométricas. No seu livro Discurso sobre o Método, escrito em 1637, aparece a célebre frase em latim "Cogito ergo sum" , ou seja: "Penso, logo existo".
1.1 - Coordenadas cartesianas na reta
Seja a reta r na Fig. abaixo e sobre ela tomemos um ponto O chamado origem.
Adotemos uma unidade de medida e suponhamos que os comprimentos medidos a partir de O, sejam positivos à direita e negativos à esquerda.

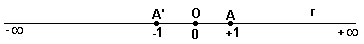
O comprimento do segmento OA é igual a 1 u.c (u.c = unidade de comprimento). É fácil concluir que existe uma correspondência um a um (correspondência biunívoca) entre o conjunto dos pontos da reta e o conjunto R dos números reais. Os números são chamados abscissas dos pontos. Assim, a abscissa do ponto A’ é -1, a abscissa da origem O é 0 (zero), a abscissa do ponto A  é 1, etc. A reta r é chamada eixo das abscissas.
1.2 - Coordenadas cartesianas no plano
Com o modo simples de se representar números numa reta, visto acima, podemos estender a idéia para o plano, basta que para isto consideremos duas retas perpendiculares que se interceptem num ponto O, que será a origem do sistema. Veja a Fig. a seguir:

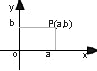
Dizemos que a é a abscissa do ponto P e b é a ordenada do ponto P.
O eixo OX é denominado eixo das abscissas e o eixo OY é denominado eixo das ordenadas.
O ponto O(0,0) é a origem do sistema de coordenadas cartesianas.
Os sinais algébricos de a e b definem regiões do plano denominadas QUADRANTES.
No 1º quadrante, a e b são positivos, no 2º quadrante, a é negativo e b positivo, no 3º quadrante, ambos são negativos e finalmente no 4º quadrante aé positivo e b negativo.

Observe que todos os pontos do eixo OX tem ordenada nula e todos os pontos do eixo OY tem abscissa nula. Assim, dizemos que a equação do eixo OX é y = 0 e a equação do eixo OY é  x = 0.
Os pontos do plano onde a = b, definem uma reta denominada bissetriz do 1º quadrante, cuja equação evidentemente é y = x.
Já os pontos do plano onde a = -b (ou b = - a), ou seja, de coordenadas simétricas, definem uma reta denominada bissetriz do 2º quadrante, cuja equação evidentemente é y = - x.
Os eixos OX e OY são denominados eixos coordenados.

Exercícios Resolvidos

1) Se o ponto P(2m-8 , m) pertence ao eixo dos y , então :
a) m é um número primo
b) m é primo e par
c) m é um quadrado perfeito
d) m = 0
e) m < 4
Solução:
Se um ponto pertence ao eixo vertical (eixo y) , então a sua abscissa é nula.
Logo, no caso teremos 2m - 8 = 0, de onde tiramos m = 4 e portanto a alternativa correta é a letra C, pois 4 é um quadrado perfeito (4 = 2²).
2) Se o ponto P(r - 12 , 4r - 6) pertença à primeira bissetriz , então podemos afirmar que :
a) r é um número natural
b) r = - 3
c) r é raiz da equação x³ - x² + x + 14 = 0
d) r é um número inteiro menor do que - 3 .
e) não existe r nestas condições .
Solução:
Os pontos da primeira bissetriz (reta y = x), possuem abscissa e ordenada iguais entre si. Logo, deveremos ter: r - 12 = 4r - 6 de onde conclui-se r = - 2.  Das alternativas apresentadas, concluímos que a correta é a letra C, uma vez que -2 é raiz da equação dada. Basta substituir  x  por   -2  ou seja: (-2)³ - (-2)² + (-2) + 14 = 0 o que confirma que   -2 é raiz da equação.
3) Se o ponto P(k , -2) satisfaz à relação x + 2y - 10 = 0 , então o valor de k ² é :
a) 200
b) 196
c) 144
d) 36
e) 0
Solução:
Fazendo x = k e y = -2 na relação dada, vem: k + 2(-2) - 10 = 0.
Logo, k = 14 e portanto k² = 14² = 196.
Logo, a alternativa correta é a letra B.

2 - Fórmula da distância entre dois pontos do plano cartesiano

Dados dois pontos do plano A(Xa,Ya) e B(Xb,Yb) , deduz-se facilmente usando o teorema de Pitágoras a seguinte fórmula da distancia entre os pontos A e B:

Esta fórmula também pode ser escrita como: d²_AB = (X_b - X_a)² + (Y_b - Y_a)² , obtida da anterior, elevando-se ao quadrado (quadrando-se) ambos os membros.

Exercício Resolvido

O ponto A pertence ao semi-eixo positivo das ordenadas ; dados os pontos B(2 , 3) e C(-4 ,1) , sabe-se que do ponto A se vê o segmento BC sob um ângulo reto . Nestas condições podemos afirmar que o ponto A é :
a) (3,0)
b) (0, -1)
c) (0,4)
d) (0,5)
e) (0, 3)

Solução: 
Como do ponto A se vê BC sob um ângulo reto, podemos concluir que o triângulo ABC é retângulo em A. Logo, vale o teorema de Pitágoras: o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. Portanto, podemos escrever: AB² + AC² = BC² (BC é a hipotenusa porque é o lado que se opõe ao ângulo reto A). Da fórmula de distância, podemos então escrever, considerando que as coordenadas do ponto A são (0,y) , já que é dado no problema que o ponto A está no eixo dos y e portanto sua abscissa é nula:
AB² = ( 0 - 2 )² + ( y - 3 )² = 4 + ( y - 3 )²AC² = ( 0 - (-4))² + ( y - 1)² = 16 + ( y - 1 )²BC² = ( 2 - (-4))² + ( 3 - 1 )² = 40
Substituindo, vem: 4 + ( y - 3 )² + 16 + ( y - 1 )² = 40 \ ( y - 3 )² + ( y - 1)² = 40 - 4 - 16 = 20
Desenvolvendo, fica: y² - 6y + 9 + y² - 2y + 1 = 20 \ 2y² - 8y - 10 = 0 \ y² - 4y - 5 = 0 , que resolvida, encontramos y = 5 ou y = -1. A raiz y = -1 não serve, pois foi dito no problema que o ponto A está no semi-eixo positivo . Portanto, o ponto procurado é A(0,5), o que nos leva a concluir que a alternativa correta é a letra D.

3 - Ponto médio de um segmento

Dado o segmento de reta AB , o ponto médio de AB é o ponto M Î AB tal que AM = BM .
Nestas condições, dados os pontos A(x₁ , y₁) e B(x₂ , y₂) , as coordenadas do ponto médio
M(x_m , y_m) serão dadas por:

Exercício Resolvido

Sendo W o comprimento da mediana relativa ao lado BC do triângulo ABC onde A(0,0), B(4,6) e C(2,4) , então W² é igual a:
a) 25
b) 32
c) 34
d) 44
e) 16
Solução:
Chama-se mediana de um triângulo relativa a um lado, ao segmento de reta que une um vértice ao ponto médio do lado oposto. Assim, a mediana relativa ao lado BC será o segmento que une o ponto A ao ponto médio de BC. Das fórmulas de ponto médio anteriores, concluímos que o ponto médio de BC será o ponto M( 3, 5). Portanto, o comprimento da mediana procurado será a distância entre os pontos A e M. Usando a fórmula de distância encontramos AM = Ö 34 ou seja raiz quadrada de 34. Logo, W = Ö 34 e portanto W² = 34, o que nos leva a concluir que a resposta correta está na alternativa C.
4 - Baricentro de um triângulo
Sabemos da Geometria plana , que o baricentro de um triângulo ABC é o ponto de encontro das 3 medianas . Sendo G o baricentro , temos que AG = 2 . GM onde M é o ponto médio do lado oposto ao vértice A (AM é uma das 3 medianas do triângulo).
Nestas condições , as coordenadas do baricentro G(x_g , y_g) do triângulo ABC onde A(x_a , y_a) , B(x_b , y_b) e C(x_c , y_c) é dado por :


Conclui-se pois que as coordenadas do baricentro do triângulo ABC, são iguais às médias aritméticas das coordenadas dos pontos
A , B e C.
Assim, por exemplo, o baricentro (também conhecido como centro de gravidade) do triângulo ABC onde A(3,5) , B(4, -1) e C(11, 8) será o ponto G(6, 4). Verifique com o uso direto das fórmulas.
Exercício resolvido
Conhecendo-se o baricentro B(3,5), do triângulo XYZ onde X(2,5) , Y(-4,6) , qual o comprimento do segmento BZ?
Solução:
Seja o ponto Z(a,b). Temos, pela fórmula do baricentro:
3 = (2 - 4 + a) / 3  e   5 = (5 + 6 + b) / 3
Daí, vem que  a = 11 e b = 4. O ponto Z será portanto Z(11, 4).
Usando a fórmula da distância entre dois pontos, lembrando que B(3,5) e Z(11,4),  encontraremos  BZ = 65^1/2 u.c.  (u.c. = unidades de comprimento).
Agora resolva este: 

Os pontos A(m, 7), B(0, n) e C(3, 1) são os vértices de um triângulo cujo baricentro é o ponto
G(6, 11). Calcule o valor de m² + n².
Resposta: 850

1 - O uso do Determinante de terceira ordem na Geometria Analítica
1.1 - Área de um triângulo
Seja o triângulo ABC de vértices A(x_a , y_a) , B(x_b , x_c) e C(x_c , y_c) . A área S desse triângulo é dada por
S = 1/2 . | D | onde ½ D½ é o módulo do determinante formado pelas coordenadas dos vértices A , B e C .

 Temos portanto:

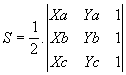
A área S é normalmente expressa em u.a. (unidades de área)
Para o cálculo do determinante de terceira ordem, utilizamos a conhecida e prática regra de Sarrus.
1.2 - Condição de alinhamento de três pontos
Três pontos estão alinhados se são colineares , isto é , se pertencem a uma mesma reta .
É óbvio que se os pontos A , B e C estão alinhados , então o triângulo ABC não existe , e podemos pois considerar que sua área é nula ( S = 0 ) .
Fazendo S = 0 na fórmula de área do item 1.1 , concluímos que a condição de alinhamento dos 3 pontos é que o determinante D seja nulo , ou seja : D = 0 .

Exercício resolvido:

Se os pontos P(3 , 5) , Q(-3 , 8) e C(4 , y) são colineares , então o valor de y é :
a) 4
b) 3
c) 3,5
d) 4,5
e) 2
Solução:

Para que estes pontos estejam alinhados (pontos colineares), deveremos ter:

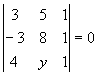
Desenvolvendo o determinante pela Regra de Sarrus, obtemos:
- 32 - 3y + 15 + 24 - 3y + 20 = 0 \ y = 9/2 = 4,5.
Portanto a alternativa correta é a letra D.
2 - Equação geral da reta.
Seja r a reta que passa pelos pontos A(x_a , y_a) e B(x_b , y_b).
Seja P(x , y) um ponto qualquer desta reta . Pela condição de alinhamento de 3 pontos , podemos escrever:

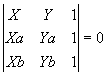
Desenvolvendo o determinante acima obtemos:
(Ya - Yb) . x + (Xa - Xb) . y + (XaYb - XbYa) = 0 .
Fazendo Ya - Yb = a , Xa - Xb = b e XaYb - XbYa = c , decorre que todo ponto P(x,y) pertencente à reta , deve verificar a equação :ax + by + c = 0 
que é chamada equação geral da reta r .
Exemplos:
2x + 5y - 4 = 0 (a = 2 , b = 5 , c = -4)
3x - 4y = 10 (a = 3 , b = -4 , c = -10); observe que podemos escrever 3x - 4y - 10 = 0.
3y + 12 = 0 (a = 0 , b = 3 , c = 12)
7x + 14 = 0 (a = 7 , b = 0 , c = 14)
x = 0 (a = 1 , b = 0 , c = 0) ordenadas .® equação do eixo Oy - eixo das
y = 0 (a = 0 , b = 1 , c = 0) ® equação do eixo Ox - eixo das abscissas .
Observações:
a) a = 0 ® y = - c/b (reta paralela ao eixo dos x )
b) b = 0 ® x = - c/a (reta paralela ao eixo dos y)
3 - Posição relativa de duas retas
Sabemos da Geometria que duas retas r e s no plano podem ser :
Paralelas : r Ç s = Æ
Concorrentes : r Ç s = { P } , onde P é o ponto de interseção .
Coincidentes : r = s.

Dadas as retas r : ax + by + c = 0 e s : a’x + b’y + c’ = 0 , temos os seguintes casos :
 ® as retas são coincidentes .
 ® as retas são paralelas .

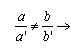as retas são concorrentes .

Exercícios resolvidos

1 - OSEC-SP - Qual a posição relativa das retas r : x + 2y + 3 = 0 e s: 4x + 8y + 10 = 0 ?

Solução:
Temos que: 1 / 4 = 2 / 8 ¹ 3 / 10 (segundo caso acima) e,  portanto as retas são paralelas.

2 - Dadas as retas r : 3x + 2y - 15 = 0 ; s : 9x + 6y - 45 = 0 e t : 12x + 8y - 60 = 0 , podemos afirmar:
a) elas são paralelas
b) elas são concorrentes
c) r Ç t Ç s = R
d) r Ç s Ç t = R²
e) as três equações representam uma mesma reta .
Solução:
Primeiro vamos verificar as retas r e s: 3 / 9 = 2 / 6 = -15 / -45 (primeiro caso acima) e portanto as
retas r e s são coincidentes.
Comparando agora, por exemplo a reta  r com a reta  t , teremos:
3 / 12 = 2 / 8 = -15 / -60 (primeiro caso acima);
Portanto as retas  r, s e t  são coincidentes, ou seja, representam a mesma reta.
Logo a alternativa correta é a letra E.
3) Para se determinar o ponto de interseção de duas retas , basta resolver o sistema de equações formado pelas equações das retas. Nestas condições , pede-se calcular as coordenadas do ponto de interseção das retas r : 2x + 5y - 18 = 0 e s : 6x - 7y - 10 = 0.
Solução:
Da equação da reta r  tiramos: x = (18 - 5y) / 2 (eq. 1);
substituindo na equação da reta s vem:
6[(18-5y) / 2] - 7y -10 = 0  \ 54 - 15y - 7y - 10 = 0 \ 44 - 22y = 0 \ 44 = 22y \ y = 2;
substituindo o valor de y na eq. 1 fica: .x = (18 - 5.2) / 2 = 4.
Portanto o ponto de interseção é o ponto P(4,2).
Agora resolva esta:
Qual a área do triângulo ABC de vértices A(2,5), B(0,3) e C(1,1)?
Resposta: S = 3 u.a. (3 unidades de área)